Due to the real-time nature of a candle chart, most of tech analysis indicators work according to principles of a sliding window technique. Indie has @algorithm decorator and SeriesF, MutSeriesF data types which help to create algorithms that use this technique. All this provides an effective and convenient way for series processing.

​
@algorithm, SeriesF and MutSeriesF

Decorator @algorithm is a syntactic sugar that can be applied to a function definition which is equivalent to writing a class definition of an algorithm inherited from indie.Algorithm class. More details about how this kind of syntactic sugar works are here.

SeriesF is a data type that represents series of numeric values like prices of some instrument. Every element of a SeriesF object stores a value at time of some bar on a chart. SeriesF objects have an interface which gives access to their values with square brackets operator. For example, series of close prices of some instrument is self.close (where self is an object with Context interface) and current (the last) close price can be accessed with expression self.close[0]. The close price at the previous candle is self.close[1] and so on.

Series objects like self.open, self.high, self.low, self.close and self.volume are built-in and read-only. But Indie lets you create your own series objects, put some values that your algorithm calculates into them and use them in the further parts of your indicator code. This is exactly what MutSeriesF type is intended to be used for.

Function MutSeriesF.new wraps any primitive number value and returns an object of MutSeriesF type with that value written into the [0] (the most recent element). This provides access to previous values of that value in the future Indie invocations. In other words, MutSeriesF data type is what you need if you want to persist some value over bars.

NOTE: MutSeriesF is a type alias for MutSeries[float] and SeriesF is a type alias for Series[float]. In future versions of Indie it is planned to support other types for element of those containers besides float.

​
SMA, Sum and sliding window technique

Now it is a good time to look at some of the algorithms in action. Let us take some very basic indicator like for example Simple moving average (SMA) and see how it works under the hood. To calculate SMA with length=4 of some price series, we have to divide every element of a corresponding sum (with the same length=4) by it’s length. That is why, first we have to look in detail how sum algorithm could be implemented.

The sum of length=4 could be calculated very simple. First, the value of sum_0 (where 0 is the bar index) is undefined, because at that point there is only one price is available in the input series. Same with the sum_1 and sum_2. But the value of sum_3 equals to price_0 + price_1 + price_2 + price_3 which is 5 + 2 + 1 + 2 = 10. So far so good and the next sum value, sum_4, equals to price_1 + price_2 + price_3 + price_4 which is 2 + 1 + 2 + 4 = 9 correspondingly. Finally, in the same manner we calculate sum_5 as price_2 + price_3 + price_4 + price_5 which is 1 + 2 + 4 + 6 = 13. And so on, this is illustrated on the diagram:

Calculation of a sum in a straightforward (but non-effective by time) way:

ctx.bar_index:      0,    1,    2,    3,    4,    5, ...
price:              5,    2,    1,    2,    4,    6, ...
                    _,  ...
                    _,    _,  ...
                    _,    _,    _,   ...
                    _,    _,    _,    10, ...
                    _,    _,    _,    10,   9,  ...
sum(length=4):      _,    _,    _,    10,   9,   13, ...

Here is Indie implementation of this algorithm:

# indie:lang_version = 4
from indie import algorithm, SeriesF, MutSeriesF

@algorithm
def Sum(self, price: SeriesF, length: int) -> SeriesF:
    result = 0.0
    for i in range(length):
        result += price[i]
    return MutSeriesF.new(result)

Reader may notice that we have to sum the same price values more than once. We may calculate the next sum values more efficiently using the sum value calculated on a previous step. For example sum_4 = sum_3 - price_0 + price_4, sum_5 = sum_4 - price_1 + price_5 and so on. This other way of calculation is exactly the mentioned before sliding window technique. It turns out that with larger lengths the second way is way more efficient in terms of time. And here is the Indie implementation of it:

# indie:lang_version = 4
from math import nan
from indie import algorithm, SeriesF, MutSeriesF

@algorithm
def Sum(self, price: SeriesF, length: int) -> SeriesF:
    s = MutSeriesF.new(init=0)
    s[0] += price[0]
    result: float
    if len(price) > length:
        s[0] -= price[length]
        result = s[0]
    else:
        result = nan
    return MutSeriesF.new(result)

NOTE: If you need a Sum or SMA you don’t have to implement them by yourself. Simply import them from the standard library like this: from indie.algorithms import Sum, Sma.

Now, after we have a Sum algorithm, it is trivial to write SMA as Sma algorithm too:

@algorithm
def Sma(self, price: SeriesF, length: int) -> SeriesF:
    s = Sum.new(price, length)
    return MutSeriesF.new(s[0] / length)

As you can see, it is very easy to call one algorithm from another. It is very natural to connect them in a sort of a chain. That is why all the functions decorated with @algorithm return SeriesF result (or tuple of SeriesF values).

Finally here is the Main entry point of our indicator that plots it on chart:

@indicator('SMA Example', overlay_main_pane=True)
def Main(self):
    result = Sma.new(self.close, 12)
    return result[0]

​
Series behavior during history vs runtime

Suppose we have an indicator that counts green bars of an instrument on a chart: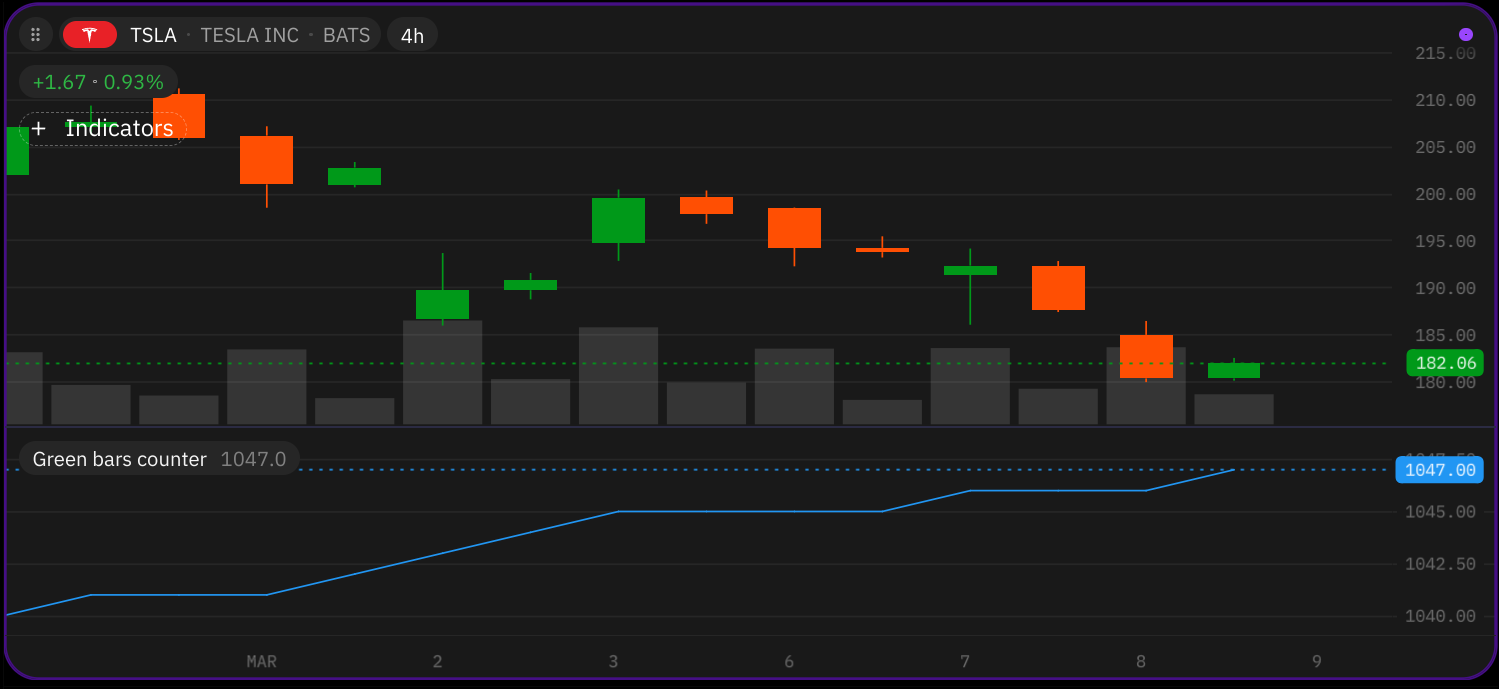

# indie:lang_version = 4
from indie import indicator, MutSeriesF

@indicator('Green bars counter')
def Main(self):
    green_count = MutSeriesF.new(init=0)
    if self.close[0] > self.open[0]:
        green_count[0] += 1
    return green_count[0]

Bar coloring traditionally works this way: if closing price of a bar is greater than it’s opening price, then the bar is green, otherwise it is red. In the Indie code we have a series green_count object which accumulates the desired count. This count is returned from Main which plots a blue line on a chart. On Figure 6.1 we see how blue line raises up by 1 on every green bar and stays flat if bar is red. First let us take a close look at how this Series object behaves during indicator calculation on a historical bars of some imaginary instrument. Close and open prices of our instrument could be for example:

time:      t0, t1, t2, t3, t4, t5
open:       9, 18,  8,  7,  8, 15
close:     12,  7, 14, 13, 12,  5

History prices open and close will be passed to the indicator for calculation one by one from left to right. Indicator will calculate, at time t0, like this ‘12 is greater than 9, so we add 1 to green_count’. On the next calculation, at time t1, it will be ‘7 is not greater than 18, so do nothing. Value of green_count is still 1’. In the end, green_count series will contain these values:

time:          t0, t1, t2, t3, t4, t5
green_count:    1,  1,  2,  3,  4,  4

Thus, during the calculation of indicator on historical data everything is simple, predictable and very natural.

Let us suppose that starting from time t6 the realtime begins:

time:          t6, t6, t6, t7, t7, t7, t7, t8, t8, t9, ...
open:           6,  6,  6, 11, 11, 11, 11,  7,  7, ...
close:         10,  2, 12, 14, 12, 16,  9,  5, 12, ...

Our indicator will behave like this:

time:              t6, t6, t6, t7, t7, t7, t7, t8, t8, t9, ...
green_count:        5,  4,  5,  6,  6,  6,  5,  5,  6, ...
last bar update:            ^               ^       ^

Moments of the final bar update are marked with ^s. They are important, because values calculated in these moments are stored in the end in the green_count series, overwriting all values written there before at the time of the same bar.

Bar usually updates multiple times at realtime. Every realtime update of a bar triggers a calculation of indicator. Right before every such calculation the state of the green_count[0] series element resets to it’s previous value (i.e. green_count[1]) — the value it had at the time of previous bar. That is why during the three updates of bar starting at t6, corresponding element of green_count series was set to 5 at first, then reverted back to 4, then finalized at value 5.

If nothing is written in the green_count[0] series element and bar finalizes then this value is carried further to the next series element without change.

​
MutSeriesF.new() function description

MutSeriesF.new(
  reset: indie.Optional[float] = None,
  init: indie.Optional[float] = None,
  size: indie.Optional[int] = None,
) -> indie.MutSeriesF

Function MutSeriesF.new creates MutSeriesF objects which are containers for calculated values in Indie code. The main feature of MutSeriesF container is ability to store (or ‘remember’) historical values of some variable, those values could be later accessed with the square brackets operator. At the moment MutSeriesF class supports only float type as series element.

Please note that MutSeriesF objects give read-write access only to the last value of the series object and read access to any (well, down to some limit) previous values.

Parameters:

  • reset — is a value that is written into the most recent element of the MutSeriesF every time MutSeriesF.new() function is executed. The effect of this parameter is the same as:
# this:
s = MutSeriesF.new(reset_val)

# is the same as:
s = MutSeriesF.new()
s[0] = reset_val
  • init — is a value that is written into the most recent element of the series object only once after the MutSeriesF object was created. Or, in other words, it is a value that is written only at the time of the first MutSeriesF.new() function call.
# this:
s = MutSeriesF.new(init=init_val)

# is similar to:
s = MutSeriesF.new()
if self.bar_index == 0:
    s[0] = init_val
  • size — is number of elements that MutSeriesF object should persist in memory. The default and minimum possible size is 2, which means that a series of size=2 stores in memory one value at the time of the last candle and another at the time of the previous candle. The size is automatically expanded during the historical calculation of an indicator. For example:
# This series allows us to get access to s[0], s[1] and s[2] elements from now
s = MutSeriesF.new(0.0, size=3)

# We can read previous value which is out of size=3, for example s[5]:
s[0] = s[5] + 1

The size of s was expanded from 3 to 6. It is allowed to get access to s[0], s[1], s[2], s[3] and s[4], s[5] elements after that. It may seem to have not very much sense at first. We set some size, but we are allowed to expand it later. Well, it is allowed to expand the size only during the calculation of indicator history. The algorithm by some reason may calculate the lookback offset for some series at runtime, depending on prices for example like this:

max_size = 100
offset = min(math.round(self.close[0]), max_size)
s = MutSeriesF.new(init=0.0, size=max_size)
a = s[offset]  # calc something with it...

We cannot predict values of self.close series. They could be less than max_size = 100 at first but then during realtime, they could rise higher. That is why we should always limit the max_offset with min and reserve the s’s size with size parameter. Otherwise the indicator would fail, since, again, we cannot expand the size at realtime.

NOTE: MutSeriesF objects also have a method request_size(new_size: int) which can be used to expand the size explicitly.

MutSeriesF.new function has a ‘get or create’ semantics. It means that only one MutSeriesF object is created per one MutSeriesF.new function call occurrence in the code. All subsequent calls of MutSeriesF.new in exactly the same position in Indie script simply return MutSeriesF objects created previously. For example:

@indicator('Example')
def Main(self):
    s1 = MutSeriesF.new(0.0)
    s2 = MutSeriesF.new(42.0)
    # ...

In this code only two MutSeriesF objects are created: s1 and s2. The Main function is called multiple times - per every historical candle and per every realtime update of the last candle — thus multiple times MutSeries.new functions are called too. But only when self.bar_index == 0 the s1 and s2 objects are created. During all the subsequent calls, s1 and s2 only receive references to existing MutSeriesF objects. If you want more details about how MutSeriesF.new function works, read this.

​
TL;DR: How to use classes from indie.algorithms package in my indicator?

Suppose we have found an algorithm (e.g. RSI) in the Indie library and want to use it in our indicator. These are the steps which should be done in order to achieve this:

  • Import the class of the desired algorithm, which in our example let it be the indie.algorithms.Rsi:
from indie.algorithms import Rsi

  • Go to the place in the code where you want to call the algorithm. Algorithms can be called either:

    In our example we go to the Main entry point function:

@indicator('Test')
def Main(self):
    # ...
    # >>> somewhere here <<<
    # ...

NOTE: that you cannot call algorithm’s new() function from global scope of indicator or from some ‘plain old python function’.

  • Call the algorithm’s new() syntactic sugar function according to it’s signature which for Rsi is new(src: indie.SeriesF, length: int) -> indie.SeriesF (here is the link) and write the resulting series of RSI values to some variable, e.g. rsi_result:
@indicator('Test')
def Main(self):
    rsi_result = Rsi.new(self.close, 12)
    # ...
  • From now you may use the rsi_result series, for example, return it from Main for plotting on chart or pass to some other algorithm for further processing. If you want just access the last float RSI value, use square brackets operator rsi_result[0].

Final version of our example looks like this:

# indie:lang_version = 4
from indie import indicator
from indie.algorithms import Rsi

@indicator('Example')
def Main(self):
    rsi_result = Rsi.new(self.close, 12)
    return rsi_result[0]

​
TL;DR: How to use indie.MutSeriesF in my indicator?

Suppose we are working on an indicator where we calculate some math formula on every candle. Let us take something simple like OC2 = (OpenPrice + ClosePrice) / 2 as an example of such a formula. Here is Indie code that calculates and plots OC2:

# indie:lang_version = 4
from indie import indicator

@indicator('Example', overlay_main_pane=True)
def Main(self):
    OC2 = (self.open[0] + self.close[0]) / 2
    return OC2

NOTE: That type of OC2 variable is float.

It could be very useful to store such a value like OC2 (or, to be more accurate, a series of values because we calculate new value on each candle) in a Series-like container (which is indie.MutSeriesF). This gives following benefits:

  • it will be possible to access historical values of OC2 (values which were calculated previously on historical candles);
  • it will be possible to process series of OC2 values with algorithms from indie.algorithms package (or our own).

Here is how to do it:

  • Import class indie.MutSeriesF to your indicator:
from indie import MutSeriesF
  • Wrap the value with indie.MutSeriesF.new() syntactic sugar static method:
OC2 = MutSeriesF.new((self.open[0] + self.close[0]) / 2)

Since this moment, type of OC2 variable is indie.MutSeriesF, which is a container with float values inside. Please note, that indie.MutSeriesF.new() method can be called either:

NOTE: that you cannot call indie.MutSeriesF.new() function from global scope of indicator or from some ‘plain old python function’.

  • Use the OC2 series in further calculations:
    • access historical values of OC2 variable with the square brackets operator. For example:
# indie:lang_version = 4
from indie import indicator, MutSeriesF

@indicator('Example', overlay_main_pane=True)
def Main(self):
    OC2 = MutSeriesF.new((self.open[0] + self.close[0]) / 2)
    return OC2[0], OC2[1], OC2[2]

Here OC2[0] returns float value of our variable on the last candle, OC2[1] - value on the previous candle, OC2[2] - value that was 2 candles back and so on.

  • process series of OC2 values with some algorithm, for example SMA, like this:
# indie:lang_version = 4
from indie import indicator, MutSeriesF
from indie.algorithms import Sma

@indicator('Example', overlay_main_pane=True)
def Main(self):
    OC2 = MutSeriesF.new((self.open[0] + self.close[0]) / 2)
    smoothed_OC2 = Sma.new(OC2, 12)
    return smoothed_OC2[0]

Was this page helpful?

Data types in IndieInput parameters